When children first start learning about subtraction, they learn that it means to “take away”. They start with a given quantity and then “take out” or “take away” the amount being subtracted. Over time, they begin to subtract multi-digit numbers and learn various subtraction strategies. Standard Algorithm is the most commonly used strategy, and the strategy most widely accepted by adults since it’s what we learned growing up.
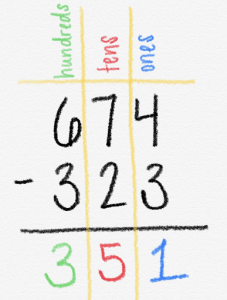The standard Algorithm seems pretty straight forward. We subtract one place value at a time, starting with the ones place, moving right to left. In the example to the right, the subtraction problem is broken up by place value. Within each place, the subtrahend, or the number being subtracted, is smaller than the minuend, or the starting quantity. This is easy for most children to conceptualize since the difference is a positive number.
Subtraction With Regrouping Misconceptions
When students begin learning subtraction with regrouping, it can feel like a whole separate giant to tackle. All of a sudden, it isn’t as clean and simple as before, and many students choose to simply switch digits between the minuend and subtrahend. For example, in 34 – 19, many students would swap the digits 4 and 9 and solve 9 – 4 = 5 to satisfy the confusion caused by trying to take a larger number from a smaller number.
Many adults teach students that they “can’t” subtract a larger number from a smaller number, and therefore they must “borrow”. There are two problems with this. First, it is completely false that a larger number cannot be subtracted from a smaller number. In the education world, we call this a “rule that expires”, meaning that the rule applies to the particular concept taught, but will no longer apply when a new concept is introduced. In this example, as soon as students learn about negative numbers, they will learn that subtracting a larger number from a smaller number is possible, and that the difference will be negative. Instead of teaching a rule and then contradicting it later, manipulatives can be used to show the child that the subtrahend is smaller than the minuend, and therefore it wouldn’t make sense to end up with a negative difference.
Second, using the term “borrow” addresses a different issue. Have you ever been told “It’s okay, you can keep it!” in response to asking a friend to borrow a tissue? The joke is that the term “borrow” implies that the item will be returned, and a tissue should clearly never be returned! The same applies to a subtraction problem that requires regrouping. The amount “borrowed” is never returned. We can easily rectify this by instead saying that we are “taking” from the next highest place value. I also like to say that the next highest place value will give to the previous place value to help it out. This concept can easily be shown through the use of manipulatives, which I demonstrate below.
The Importance Of Manipulatives
Manipulatives are consistently used in classrooms to help illustrate various concepts. They are especially useful for visual and kinesthetic learners and can be particularly effective when used as scaffolding for struggling students. Manipulatives provide a physical representation of a concept that concretely helps students visualize how it works. Teachers can use these manipulatives to model concepts and students can use them to work through problems using strategies modeled by the teacher.
There are a wide range of manipulatives that can be used for any given topic, but base ten blocks are a teacher favorite and are used to teach many standards under the Number and Operations in Base Ten domain. Most schools provide teachers with class sets of base ten blocks similar to these, but it’s very easy for parents to make their own set using paper and scissors.
DIY Base Ten Blocks
I kept these base ten blocks very basic. I simply cut up a few old folders and wrote the correct numbers on each piece. Color coding the blocks is a helpful scaffold, but black and white blocks will work too. Here is a link where you can download a free printable color-coded and black and white base ten blocks.
Step-By-Step Example
The images shown below demonstrate how to practice subtraction with regrouping using the base ten block manipulatives I made.
There are three main components to this process:
- The written equation
- The base ten blocks depicting the minuend
- The “bank” of extra base ten blocks that will be exchanged with parts of the minuend during the regrouping portion of this strategy.
The placement of the “bank” is shown on the whiteboard for demonstrative purposes, but when practicing with a child, the adult acts as the “bank”. As an extra scaffold, I’ve written the subtraction equation so that the color of each digit matches the color of its corresponding place value block.
Step 1: Write the equation and request the appropriate blocks.
Have your child request the base ten blocks needed to create the minuend. The request of the appropriate quantity of base ten blocks is an important step, as this will demonstrate the child’s understanding of the place value and value of each digit.
Step 2: Regroup.
If your child is comfortable with subtraction without regrouping, they will know to start with the ones place and will also understand that subtraction means the subtrahend should be “taken out” of the minuend. This will present your child with a conundrum: there aren’t enough ones blocks to take out the appropriate amount.
This is where the bank comes in. You present an opportunity to rectify the issue by offering to make an exchange. Try and allow your child to independently determine that one tens block should be traded for ten ones blocks. If a student is struggling, instead of telling them exactly what to do, guide them by asking how the next place value could “help out”.
Step 3: Record the changes made.
It is important for children to see how the process is shown on paper, since this is ultimately how they will be showing their work. Use this opportunity to explain how to show that a ten was taken from the tens place and decomposed in order to give ten ones to the ones place. This helps students develop a conceptual understanding instead of a procedural understanding of standard algorithm.
Step 4: Subtract the ones place.
Now that there are enough ones to “take out” the subtrahend, have your child physically remove the appropriate number of ones blocks from the minuend and record the difference.
Step 5: Continue this process until you’re done!
A More Challenging Example
Once students understand how subtraction with regrouping works, it’s time to present a new challenge. Students at this point are used to relying on the adjacent place value to “help out” when it’s time to regroup. But what happens when there’s nothing to give?! Seeing a zero in the next place can be daunting for students and they might have difficulty figuring out how to proceed with the problem. Using the base ten blocks will show your child that the process is very similar, with only a minor difference.
Steps 1-3 are exactly the same. Write down the problem, have your child request the appropriate blocks to make the minuend, and initiate the “exchange” when it is discovered that there aren’t enough pieces to remove the appropriate amount from the minuend.
The only difference is that step three has two parts. Since there aren’t any tens to help out the ones place, we’ll have to continue to the hundreds place. Some children may suggest that one hundreds block be exchanged for one hundred ones blocks, a valid, but timely, suggestion. My response is to act overwhelmed by how long it would take to count out that many blocks and ask what other exchange can be made that would be a bit easier. This leads the student to realize that the hundreds block can be exchanged for ten tens, which we then record.
“Now do we have enough tens to help out the ones place?” I ask next. Your child has now arrived at a familiar step and should feel comfortable handing you a tens piece in exchange for ten ones pieces. Once the trade has been made, record the changes made again.
Solving the rest of the problem will feel much more natural since subtracting is all that’s left!
Conclusion
It’s no secret that math is taught differently today than when we were growing up. Although this can feel frustrating for parents, the goal of these “new” methods is for students to develop a deep conceptual understanding by building connections across topics and using previously learned concepts to better understand new, unfamiliar concepts. Standard algorithm is the same process we learned, but by purposely selecting the language used and introducing a visual component via manipulatives, children will understand how and why regrouping works, not just the steps needed to solve the problem.
- How To Practice Subtraction With Regrouping - January 14, 2020